怎么理解万有引力的本质是空间的弯曲？

广义相对论似乎认为万有引力是不存在的，取而代之的是时空的弯曲。那么时空的弯曲为什么会把树上的苹果“拉”向地面呢？弯曲的时空是怎么让平抛的物体沿着抛物线运动的呢？有没有通俗易懂的解释。不要用一个大球把膜压弯的模型来解释，小球在凹陷的膜上向大球靠拢还不是靠重力？

这个问题, 很可惜包括高赞回答在内的所有的回答, 都没能直观地解释时空弯曲具体如何产生引力, 或者说时空的弯曲方式具体如何导致测地线向下偏转,
但本回答会对此给出一个半定量并且直观的解释.
第3部分那张图片里的那种直观理解方式是我自己想到的, 反正之前别的地方没见过.
1.先从狭义相对论开始

狭义相对论时空观中两个最主要的特点, 其一就是某参考系下同时的两个事件在另一参考系下未必同时, 其二就是不同参考系下光速不变.
具体来说, 狭义相对论下不同观察者之间的参考系变换(洛伦兹变换)具有如下图的形式:


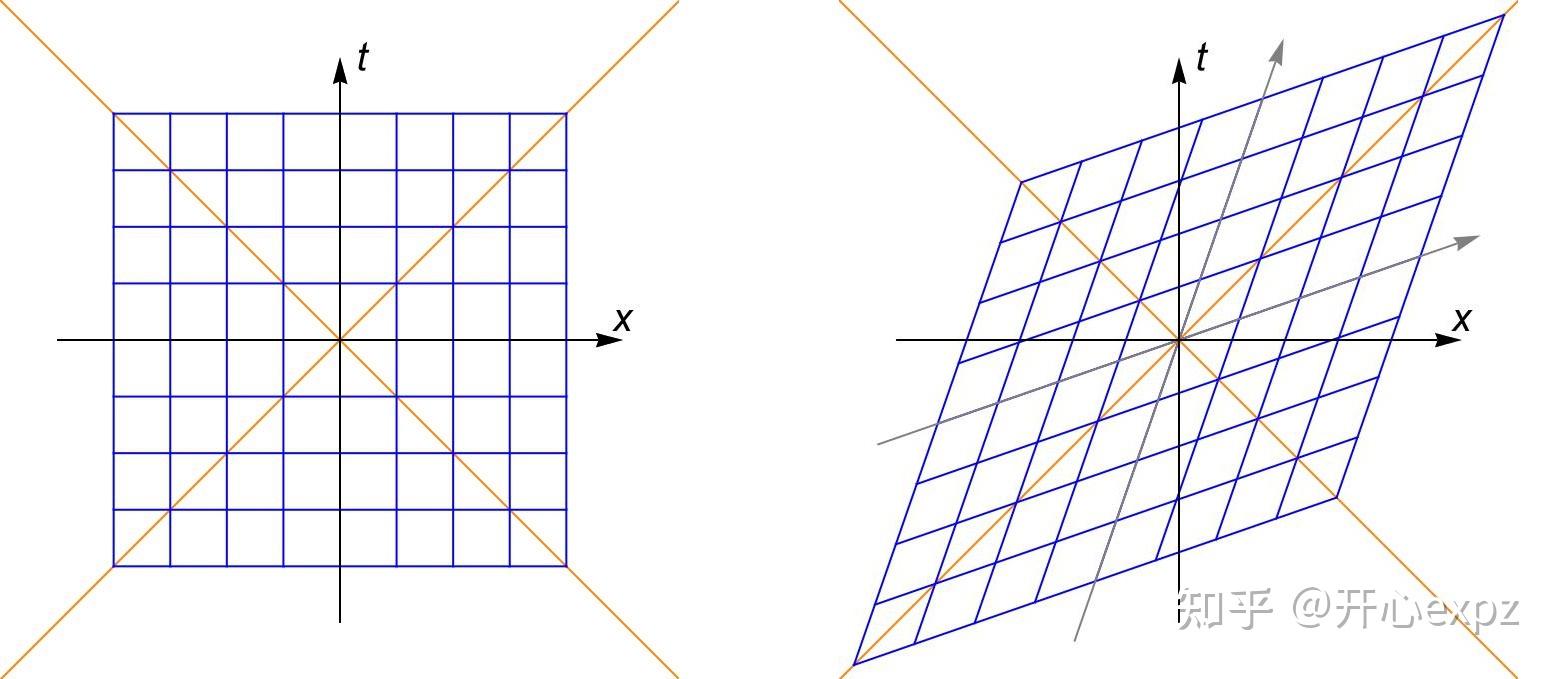
图中橙色的45°斜线就是t=0时经过原点的光在时空中的轨迹, 可见光速不变.

请记住并熟悉这个变换的样子,  后面还要用到.

而且结合光速不变与基本的对称性, 可以推出, 时空距离平方 是一个在不同参考系下不变的量,其中 是两个时空点的坐标差,
上式的一个特例就是 的情况, 此时 , 根据勾股定理可以知道, 光正好可以从一个时空点到另一个时空点, 对应光速不变.
这个时空距离在狭义相对论四维时空 (闵可夫斯基时空) 中的地位, 就相当于我们熟知的欧氏空间距离在欧氏几何中的地位, 而洛伦兹变换保持时空距离不变, 因此洛伦兹变换在四维闵氏时空中的地位就相当于是一种旋转, 称作伪转动(Boost).  
2.再来说说广义相对论的时空弯曲到底是怎么个弯曲

暂时把前面时空的概念放在一边, 先来考虑弯曲的空间是什么:
说到弯曲的空间, 可能大部分人想到的就是三维空间中的二维曲面这种嵌入的图像, 但对于曲面上的二维居民来说, 有时即使曲面在三维空间中的形态不同, 他们感受到的这上面的几何也没有任何差别, 比如说一张平坦的纸卷成筒状不会改变上面的几何, 三角形内角和照样还是180°.
我们可以用一种方式来描述曲面上的二维居民所感受到的几何. 在这个平面上建一个(曲线)坐标系, 第 个坐标值是 (上标的 不是次方), 那么某一点附近坐标差为 的, 两个很接近的点之间的距离微元平方可以写成 .  这个度规 可以随空间坐标而变化.
其中对于欧氏空间的特例, .
对于曲面上的二维居民而言, 曲面上距离微元的表达式就代表了曲面上一切的几何性质. 进一步地, 推广到一般的弯曲空间上, 我们可以认为这个距离微元的表达式才是最基本的, 并且不需要认为存在某个所谓"更高维的空间", 使得弯曲空间嵌入其中, 这种描述方式我们称之为内蕴的观点.
不过在广义相对论中, 弯曲的是整个时空(而非空间), 前面描述弯曲空间的方式, 同样可以推广到弯曲的时空, 此时用于描述其中的几何的, 是类似于闵可夫斯基时空中时空距离那样的时空距离微元.
对于平直的时空, 也就是闵可夫斯基时空的特例, .
在引力场很弱时, 这个时空很接近平直的时空. 此时, 两个很近的点之间的时空距离微元跟闵氏时空的情况相比, 只有微小的变化.

为了简单起见后面主要都考虑弱引力场的情况.

如果具体到一个星体附近的引力场的话, 那么时空弯曲情况就是: 相同固有时间对应的坐标时间变长, 径向上相同固有长度对应的坐标长度变短, 而且弱场近似下时间变长/距离缩短的程度正比于引力势能. (此处"固有时间/长度"指的是相对星体静止观测者感受到时间与距离, 同时也就是由时空距离 给出的时间/长度)
广义相对论说万有引力的本质是质量物体导致时空弯曲，那么弯曲的方向是什么呢？3.那引力又是怎么来的呢?

在很多科普中都有说到, 物体在弯曲的时空中沿着测地线运动, 其实这里测地线指的就是两点之间(按照时空距离微元算出的)长度最短/最长的曲线, 或者说一个矢量沿着自身方向平移得到的曲线.
那更具体一些, 是时空的哪种弯曲方式产生的引力呢?
先上结论, 对于低速运动的物体, 影响物体运动的主要因素 (同时也是引力的来源), 在于时间流逝快慢随空间分布的不均匀性, 而且物体受到的引力引力指向时间流逝更慢的地方.

这里所谓的时间流逝更慢, 指的是相同坐标时对应的固有时更少.

这更能看出, 通常的科普里用把膜压弯的图像来解释引力是完全不对的, 因为弯曲的膜强调的是空间的弯曲, 但真正产生引力的, 是时间的不均匀性.
不过相信大部分人看到这里就更觉得奇怪了, 时间的不均匀性怎么就会让测地线偏转了呢?
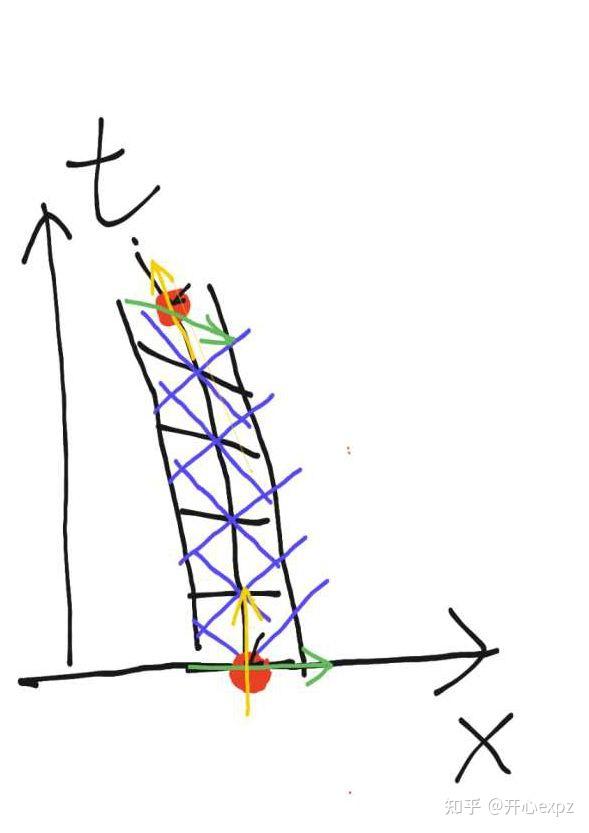
没错, 关键的地方来了, 请看下面这张图. 下图展示了一个初始静止的林檎受到向左的引力而加速的过程. 图中左边的时间流逝比右边的慢一点点. 黄色和绿色的箭头是林檎附近小范围的坐标架, 并且黄色箭头正是林檎在时空中前进的方向, 而蓝色的线是经过各个时空点的光的轨迹(即光锥).
随着时间流逝, 林檎在时空中沿着测地线运动, 可以看成是将坐标架沿着黄色箭头方向平移. 注意了, 由于左边比右边时间流逝更慢, 当坐标架向时间正方向进行平移时, 绿坐标轴的左右两端在经历了相同固有时间的情况下, 左端比右端走过了更多的坐标时间, 因此平移过程中绿坐标轴会按照图中黑色水平方向短线那样逐渐倾斜. 然后, 考虑到引力场很弱, 时空距离微元的表达式跟闵氏时空很接近, 因此时间流逝不均匀(从而使绿坐标轴倾斜)的效应, 其实"推动"着坐标架进行了一个伪旋转. 按照前面展示过的伪旋转图像, 相应地黄色坐标轴就会向左偏转, 从而时空中的运动轨迹就会按照中间那条黑线那样"弯曲", 也就表现为受到引力而加速了.


顺便一提, 同样是弱引力场, 当物体的速度与光速可比时, 空间弯曲的效应就与时间不均匀产生的效果程度相当了. 比如说, 考虑光线经过星体附近时偏转的角度这个问题, 牛顿力学下算出来的结果是广义相对论算出来的一半. 这正是因为牛顿力学只考虑到了时间不均匀性对应的那种"引力"效应, 而广义相对论除此之外还算上了空间弯曲的影响. 这个在 @金白石 的回答中也有提到.
更多内容:
在距黑洞视界线 1 米的地方向黑洞内伸一根 2 米长的棍子会怎样？

首先纠正题主的一句话，就是第一句“广义相对论认为万有引力不存在”，这是一句人云亦云的话，实际上不是这样。当我们在谈论“xx力”的时候，说的其实就是物质之间通过某种场进行相互作用。你说万有引力不存在，难道是在说两个物体之间不能通过引力场进行相互作用吗？显然不对，即使是在广义相对论中，相互作用也是存在的，在弱场近似下相互作用拉氏量可以写成下面这个样子：

那么“引力本质是时空弯曲”这句话是什么意思呢？就是说，可以直接用时空度规来描述引力场。我们知道一个事实：在引力场中自由下落的物体和一个不受力的处于惯性系的物体没啥区别（等效原理）。这意味着我们总可以通过时空坐标变换来消除引力场的影响。而在黎曼几何当中有这么一条定理：对无挠黎曼时空中的任何一点都可以找到一个坐标变换使得那点的Christoffel符号的所有分量变为零。同时，Christoffel符号为0时物体走直线（惯性运动）。这两个原因使得我们考虑Christoffel符号就是引力场强。而计算Christoffel符号只需要提供时空的度规，所以前面说可以用时空度规来描述引力场。
那么时空弯曲或平直是什么意思呢？我们定义时空度规为

的时候时空是平直的，这种情况下时空中是没有物质的。而一旦时空中有了物质，根据爱因斯坦场方程，时空度规就会偏离以上这个度规，从而使得时空成为弯曲的。
做一个总结：在广义相对论中，引力场强是Christoffel符号，这个东西取决于时空的度规，而有物质的时空的度规会偏离平直时空的度规，因此说引力的本质是时空弯曲。

我觉得首先要破除一个问题：
时空张量模型并不是广义相对论的最直观的模型，它反而是最不直观的模型，但是他是数学上最简单的模型。

最直观的引力模型就是万有引力公式，我们可以加入大量的广相修正让他看起来很复杂但更精确的拟合。但是最简单的模型就是时空张量……


所以最好的方式就是理解为这是数学上最简洁的模型就可以了，毕竟我们都知道数学上的简洁和直观一般是互斥的……
一定要直观的去了解数学上简洁的模型我觉得并不是解决和学习问题的最佳途径。例如如何直观的理解高维空间？如何直观的理解五元一次方程？与其直观的想象五维空间，还不如直接套矩阵计算来的简单……


如果你一定想要直观的了解，那么可以这样：
在一张纸上画两条平行线，
平行于线的轴是时间轴，垂直于线的是空间。
如果时空是平直的，那么这两根线就是平行的，这代表着两个东西随着时间的流逝其相对位置不会发生变化。
这时候你把线的一头的纸给捻到一起去，你就会看到这两根线变得弯曲最终合并到一起，这表示俩东西随着时间的流逝会碰一起去……

把时空张量理解为空间扭曲（丢了时间），这显然是中了那一堆所谓的直观科普的毒……

（长文，多图预警。上一篇写数学物理方程我帮着吹了一堆法国人，这篇介绍广相的是妥妥的德吹，里面大部分都是德国人。）
关于时空弯曲的科普

首先，弯曲的不仅仅是空间，而是四维的时空。对于相对论来说，时空是一个整体。按照物理学的术语来说，平直时空被称为“闵可夫斯基空间”。而弯曲的意思是说，平直的闵可夫斯基空间的度规（metric）发生了变化。
其次，广义相对论认为，是物质的质量让时空产生弯曲，而物体沿着四维时空的最短路线运行（测地线运动），其运动的形式表现为万有引力。
拿苹果做例子吧。苹果落地，牛顿说：哦，这是因为地球的引力把苹果给拉到地面上来了。
爱因斯坦说：不是的。是地球的质量使得地球周围的四维时空产生弯曲，苹果（物理术语叫做测试粒子）从树上落下，在四维时空里看来，苹果走了从树上某点的某时刻，到地面上某点某时刻的最短距离，也就是苹果按照四维测地线在运动。这个四维的测地线运动在三维空间的投影，就是大家看到的苹果从树上落下的运动。
如果还不理解，可以想象一下：如果去掉了地球，时空不弯曲了（忽略别的宇宙天体产生的时空弯曲），在平直的时空中，苹果的测地线将是一条四维的直线，之前干嘛之后还是干嘛。把这条四维直线投影到三维空间中，将是静止运动或者依旧是一条直线，这就是传说中的——牛顿第一运动定律——不受外力的苹果一直静止或者匀速直线运动。
（2021-6-17记：最后一节基于评论区的问题，又补充了一点关于苹果落地的讨论）

以上是不使用数学可以说的科普描述，如果还要深入理解，只能写上测地线方程了。
另外，不但质量可以使得时空弯曲，电荷和电磁场也可以使时空产生弯曲。所以，说得比较专业一点，是物质的“能量动量张量”使得时空发生了弯曲。
最后来说一个趣事（段子）。很多科普书会用光线偏转来表现时空的弯曲，比如下图，星光通过太阳的引力场发生偏折（下面好些答主也贴了类似的图）：



其实，不需要广义相对论，只用牛顿力学+牛顿光学（颗粒说），也可以解释光线在引力场的偏转。比如下面这位叫做Soldner的老哥，早在1801年就可以计算光线的偏转，算出来刚好是广义相对论给出的一半：


后来，是英国天文学家爱丁顿利用1919年日食的机会，测出了光线的偏转角，证明按照牛顿理论的计算是错的，爱因斯坦的计算是对的，从而为验证广相提供了极为有力的证据。
然而，然而，然而（重要的事情说三遍），爱因斯坦同学曾经在1911年就计算过引力场下光线的弯曲，并且得到了和Soldner一样的结论，嘿嘿，铁证如山：



爱因斯坦1911年的论文《关于引力对光传播的影响》

所以当爱因斯坦刚推出光线在引力场弯曲的计算时候，有不少人干脆认为爱因斯坦剽窃了19世纪初Soldner的结果。要是爱丁顿1912年就去测日全食，爱因斯坦直接就game over了，广义相对论必然会胎死腹中。
（2021-6-17记：最后一节基于评论区的问题，又补充了一点关于光线偏转的讨论）
一直到了1915年，爱因斯坦在数学家希尔伯特的神助攻下终于写出正确的引力场方程，这才把通过太阳的光线偏转角算对（后面会详细说这事儿）。



爱因斯坦（左）和希尔伯特（右），谁先得到了正确的引力场方程？

上面这个故事告诉我们一个道理：算错了不要紧，只要赶在别人做实验之前修改出正确答案，依旧是牛人。
以上是科普和八卦故事，下面来说一点更深入的。
美国人写科普，特别不喜欢写任何数学公式，表示专门写给普通人看，结果把科学写成了神神叨叨的。其实，写科学尤其是介绍物理学，必须要写公式的。下面就是给有点物理素养的朋友们看的，帮助大家理清广义相对论的历史发展历程。广义相对论，不只是爱因斯坦一个人的贡献，而是有诸如高斯、黎曼、黎曼的followers、赫兹、庞加莱、闵可夫斯基、格罗兹曼、希尔伯特、爱丁顿等等很多人的贡献，过度炒作爱因斯坦而忽略别人，比较适合大众，不适合真正学物理的人。
下面先从平直空间和弯曲空间说起。

平直空间和弯曲空间

两维和三维的平直空间很多时候也被称为欧几里得空间，这还要从勾股定理和欧几里得说起。
勾股定理告诉我们，直角三角形的斜边（c）和两条直角边（a和b）满足：
这条定理被用到解析几何里，就成为计算两点距离的基本公式。我们考虑两维的平面上两个点 (x1, y1)和 (x2, y2)，那么它们的距离就是： ，或者按照微元的形式写成：

由于公元前300年左右希腊化时代亚历山大港的欧几里得对平面和立体几何的巨大贡献，我们把这样的距离表述称为欧几里得距离，而欧几里得距离适用于平直空间，也就是欧几里得空间。下面是欧几里得（想象图）和他的《几何原本》：


其实我很期待咱们国人把欧几里得平直空间称为“商高空间”，毕竟对于国人来说勾股定理是和商高联系在一起的：



商高定理

回头再说欧几里得。现在一般把平面和立体几何的开山鼻祖说成是欧几里得，把三维平直时空说成欧几里得空间。但是，对欧几里得本人来说，并没有那么简单。老欧把平面和立体几何的命题归总在《几何原本》里，另外，作为天文学家的欧几里得，还写过关于《球面几何》的著作，题为《现象》， 下面是欧几里得《现象》的英语译本中的一页，请注意这本著作是和《几何原本》一样古老的，有2300年左右的历史了：


很明显，球面几何和平面、立体几何是不同的几何学，而且从历史上来看，很有可能球面几何比平面几何还要古老。对于球面几何来说，“直线”是球上的大圆弧，平行公理不成立，三角形内角和大于180度等等。
欧几里得的球面几何和球面天文，经过几百年的发扬光大，被希腊最伟大的天文学家托勒密整理发展，系统编写在《数学汇编》也就是《至大论》里，后来对15世纪的哥白尼影响深远。



托勒密同学，球面天文和球面几何的集大成者

回过来说球面。
球面，本质上就是一个弯曲的二维平面。从解析几何的思路来看，球面上的距离，可以写成：

其中 r 是球面的半径。这个公式描述了一个弯曲的球面上的距离微元公式。
当然，在哥白尼乃至于之后好几百年的时间里，人们并不区分什么“平直”和“弯曲”时空。一直到了19世纪初，天才数学家高斯基于天文和大地测量的考量，系统地研究了曲线和曲面，也就是1维和2维的弯曲空间，并用“曲率”来描述1维、2维空间的弯曲程度。
下图就是号称史上三大数学家之一的高斯（按照现在的说法，简称高神）：



高神

高神用“曲率”来描述曲面的弯曲程度，简称高斯曲率，比如下面三种曲面：


最左边的“束腰型”的曲线具有负的高斯曲率，中间的圆柱体曲面的高斯曲率为零，而最右边的球面具有正的高斯曲率。
如果大家对高斯曲率还不能理解的话，高神还用了另外一个量来描述曲面的弯曲程度，那就是三角形的内角和，正曲率的曲面上三角形内角和大于180度，负曲率的曲面上三角形内角和小于180度，而平直平面上的三角形内角和等于180度：


以下是高神1827年《曲面的一般研究》讨论三角形内角和的原始文献（英译本）：


关于三角形内角和和曲率之间的关系，今天称之为高斯-博内公式，也就是微分几何的基础：


有了高神曲面论系统地讨论了弯曲的二维空间，随后弯曲空间的概念就这样呼之欲出了。而奠定普遍弯曲空间理论的，则是高神的一个神人弟子，也就是黎曼。

黎曼和赫兹

1853年，也就是高斯去世前两年，高斯让他的学生黎曼，做一个关于几何学基础的演讲。于是黎曼同学小宇宙爆发，做了一个《论作为几何基础的假设》的演讲，被认为是开创了新的几何学，也就是“黎曼几何”。
下面就是传说中的黎曼同学：



当时的情况是，非欧几何的运动方兴未艾。这里对于非欧几何缘起的讨论就不多展开了，比如罗巴切夫斯基几何学，我们就看高斯——黎曼这条德国线。
黎曼在这篇著名的报告里，正式提出了高维的内蕴几何学的概念，统一了当时各种几何学。
什么叫做内蕴几何学？
我们还是回头来看距离的公式。上一节里我说到两维的距离微元ds，包括平面和球面上的距离ds。这回我们来看看三维的情况。很明显，欧氏空间（改成“商高空间”的时候，家祭无忘告乃翁）：

下面说一个比较难想象的距离，也就是在“四维球面”上的距离。我们通常说的球面，是一个在欧几里得空间里到原点距离为r 的一个三维球的表面上，也就是三维球面。我们想象一下，在四维的欧几里得空间里到原点距离为r的一个四维球的表面，也就是一个四维球面。
如果还是不理解四维球面，其实也无所谓，反正我告诉你，我可以构造一个弯曲的三维空间，这个三维空间的名字叫做“四维球面”，在这个三维空间里的距离微元：

请注意，上面那个空间的曲率就不是零了，不是一个平直的三维空间了。
黎曼把上面关于距离的公式推广到了N维的空间，其一般的形式为：

其中标记 都是从1到N的求和。微分几何里为了避免写满求和Sigma的符号，于是把上式简写成：
也就是说，N维空间，可以用一系列的 来表示，还可以写成矩阵形式，这便是空间的度规。简单地说，这种描述空间的方法，被称为“内蕴几何”。
黎曼死的早，没有能及时发展他的几何学观念，甚至连上面那篇文章也是他死后才发表的。后来有一批数学家，觉得黎曼的思路很好玩，按照黎曼的思路发展出一套几何学，被称为黎曼几何学。请注意，黎曼几何学源于高斯基于天文系和大地测量思考而发展的曲面论的高维推广，以及把非欧几何统一起来的想法，前者是物理，而后者是纯粹的数学思辨。
关于黎曼几何学的故事还可以写不少，不过都是数学的故事，我先打住。我们还是来看看黎曼几何学在物理里的运用。
现在一般科普书都说，爱因斯坦把黎曼几何学用在了广义相对论上，换句话说，老爱把数学家发展的数学游戏，变成了解释描述宇宙的工具。其实，事实并没有那么简单。
事实上，第一个把物理学几何化的同学，叫做赫兹，也是一个德国物理学家。
赫兹出生于高斯死后。如果说高神是第一代，黎曼是第二代，那么赫兹就是妥妥的德意志第三代人。今天我们总是把赫兹和电磁波的发现联系在一起（今天电磁波的频率单位就是赫兹）。其实赫兹是一个全能型的物理学家，不但做实验，也是极其卓越的理论家。他还有一部极为重要但是被后世忽略的著作，那就是他死之后发表的《力学原理》。


赫兹认为，空间、时间和物体的质量，才是力学中的基本的可以被观测到的量，而“力”的概念只是一个应该被除去的形而上学的概念。那时候的力学经历了牛顿、拉格朗日和哈密顿的发展，“力”已经不再是力学的最基本的物理量，而只是一个被定义的、运动学中的中间量。
赫兹从高斯的力学原理出发（又是高斯），发现在一定条件下，求解一个N体的力学系统，就是等价于让以下的作用量最小化：

其中 是物体的质量，而ds为

是一种黎曼度规。换句话说，赫兹的力学建立在空间、时间和质量上，把力学模型建立在一个3N维的超空间中，而该空间的度规只和物体的质量分布有关。力学的法则，被赫兹转化成为3N空间中的最小曲率问题，系统在3N空间中沿着测地线运动。这种思路被称为力学几何化，已经具有了广义相对论的雏形了。
当然，赫兹的力学和广义相对论还有很大的不同。最大的不同点就是，赫兹力学建立在多体系统3N维度的空间之中，而不像广义相对论建立在四维时空中。而且，赫兹力学里并没有把引力囊括在内。

狭义相对论，闵可夫斯基空间和协变性

要想真正理解广义相对论里所谓的时空弯曲，首先还是要理解狭义相对论，特别是闵可夫斯基空间和其空间中的协变性。
狭义相对论里，一个重头戏当然是洛伦兹变换。考察下面两个坐标系，xyz坐标系是基础坐标系，x'y'z'坐标系是相对于xyz以速度v运动的坐标系：


那么从xyz的坐标到x'y'z'的时空变换，即为洛伦茨变换：


或者可以写成矩阵的形式：


其中

爱因斯坦提出狭义相对论后没有多久，法国数学家庞加莱就发现，在洛伦兹变换下， 是一个不变量。又过了几年，爱因斯坦曾经的物理老师闵可夫斯基提出了以他名字命名的空间。
闵可夫斯基是大数学家希尔伯特的好基友，两人都来自哥尼斯堡，都成为了大牛数学家。有意思的是，在物理上，闵可夫斯基是和狭义相对论联系在一起的，而希尔伯特是和广义相对论联系在一起的。下图是两人和家人在一起：


其中膝盖上放着帽子的大头，就是闵可夫斯基，而最右侧斜躺着的那人，则是希尔伯特。
闵可夫斯基对他学生爱因斯坦的印象并不佳，称爱因斯坦为“懒惰的狗”（不过貌似爱因斯坦对闵可夫斯基的印象也不好，彼此彼此）。闵可夫斯基后来调到了哥丁根大学，和希尔伯特团聚了。他在1908年提出了把三维空间加上一维时间合成一个四维时空，这便是闵可夫斯基空间。



闵可夫斯基

下图是经常用到的闵可夫斯基空间里的“光锥”：


总的来说，光锥（Light cone）是闵可夫斯基空间下能够与一个单一事件通过光速存在因果联系的所有点的集合。
在闵可夫斯基空间中，通过洛伦兹变换，c^2*t^2 - x^2 - y^2 - z^2是不变的。也就是说，距离的微元：

在洛伦茨变换下是一个不变量，其中 被称为“固有时间”。
接下来，我们看看麦克斯韦方程在闵可夫斯基空间里的表述方式。通常情况下，我们可以把麦克斯韦方程写成（积分和微分形式）：


上面是我们经常使用的麦克斯韦方程。
所有的麦克斯韦方程，可以在闵可夫斯基空间中写成统一的形式：




其中 对应于闵可夫斯基空间的张量，即是所谓的电磁张量：


而 是闵可夫斯基空间中的四维坐标： 。
我们说麦克斯韦方程对于洛伦兹变化是协变的，意思是说，在洛伦茨变换下，坐标变换为：

虽然电磁张量要经过一系列变换， ，但是方程的形式依旧是不变的，也就是方程在洛伦茨变换下依旧是如下的形式：

这就叫做狭义相对论变换下的物理方程的协变性。
闵可夫斯基空间为狭义相对论提供了强大的数学工具。而广义相对论，也正是从闵可夫斯基空间出发的。
广义相对论的思路

狭义相对论里并没有引力，所有的物体是在四维的闵可夫斯基空间里运动，而闵可夫斯基空间的度规为：

科普书里常说的平直时空，说的就是闵可夫斯基时空。
爱因斯坦思考了一个问题，如何把引力加入到闵可夫斯基空间？
一个顺理成章的想法是，把牛顿的万有引力公式推广到四维的形式，就像上一节把麦克斯韦方程写成狭义相对论协变的形式。闵可夫斯基“四维力”的形式是：

带入万用引力公式：

很明显的一个问题是，上面的引力公式，在洛伦茨变换下不是协变的。也就是说，在坐标变换下，上面的引力公式并不能保持相同的形式，牛顿的引力定律不是相对论协变的，无法和狭义相对论统一起来。
爱因斯坦的初始问题是，如何写出一个在坐标变换下协变的引力方程？
爱因斯坦的启发来自于奥地利物理学家马赫，马赫同学作为一个实证主义者，认为引力不是形而上的存在，而是通过物体的加速度来表象出来的。也就是说，加速度和质量（惯性质量）可以把引力给代表了。爱因斯坦把这个思路称为“马赫原理”（尽管马赫坚决不承认自己和相对论有任何瓜葛。）



马赫同学

考虑下面一个自由落体的电梯。


爱因斯坦思考了非常类似于上面的“自由下落电梯”问题。我们知道，地球对于电梯里的人是有引力的，但是在自由下落的电梯里，人处于失重状态，感受不到引力，可以被当做一个惯性参考系。从坐标变换的角度来说：
地面上的参考系 ---> 电梯里的参考系
对应于：
具有引力的时空 ---> 闵可夫斯基空间
从数学的角度来说，闵可夫斯基空间具有的度规为（前面写过）：

那么对于一般的具有引力的参考系，是否可以用一个普遍的时空度规形式：

通过坐标变换，可以变回闵可夫斯基空间的 度规？
在闵可夫斯基空间里，一个物体的运动可以用四维直线来表示，而回到坐标变换前的参考系，那么物体的运动就是原参考系时空的一条测地线，也就是，坐标变换使得：

• 地面上的参考系 <---> 电梯里的参考系
  
• 具有引力的时空 <---> 闵可夫斯基空间
  
• 在时空中走测地线 <---> 四维直线
  

爱因斯坦的思考，已经把引力和时空弯曲联系到了一起。平直的闵可夫斯基空间可以通过坐标变换，变成一个扭曲的时空，而这个时空里就会出现引力。
不过爱因斯坦的思考到这里，就没法再进行下去了。换句话说，当爱因斯坦把物理思考转化为纯数学问题后，他就进行不下去了。这个问题困扰了他好几年。


这时候，一个神助攻出现了，那就是爱因斯坦的老同学，人生中的贵人，一个叫做格罗兹曼的匈牙利犹太人：



格罗兹曼


可能是由于犹太人的友谊，又可能是由于上辈子的爱情，我们来看看格罗兹曼给爱因斯坦带来的各种帮助：

• 大学里给翘课的爱因斯坦抄课堂笔记和作业
  
• 找爸爸帮毕业即失业的爱因斯坦同学找了专利局的工作，从而爱因斯坦可以业余写一堆论文
  
• 帮助爱因斯坦调回苏黎世工业大学任教
  
• 和爱因斯坦一起讨论广义相对论的雏形
  
• 帮助爱因斯坦完成广义相对论的数学部分
  
• 在爱因斯坦功成名就以后死掉了，让爱因斯坦独得各种声誉
  

怎么样？如果你这辈子觉得怀才不遇或者学物理被迫改行的话，很可能就是因为你的命里没有遇到格罗兹曼这样的好基友。



格罗兹曼和爱因斯坦，一对好基友。可惜现在为了突出神话爱因斯坦，把格罗兹曼总是忽略了。

当爱因斯坦在格罗兹曼的帮助下调到苏黎世任教后，他便去找好基友，说自己正在思考广义相对论，其中有种种困难。
格罗兹曼说，我k，老弟，你数学不行啊。使得一般空间 变成闵可夫斯基空间 的全局坐标变换是不存在滴，但是局部坐标变换是可以滴，这不就是黎曼几何吗？黎曼和他的follower（传说中的诺贝尔的情敌）早就研究了很多年了。格罗兹曼是几何学特别是非欧几何的行家，于是，他向爱因斯坦教授了黎曼几何的基础知识，广义相对论这才走上正轨。
1913年广义相对论的开山之作《广义相对论和引力论纲要》是由爱因斯坦和格罗兹曼合作的，其中二分之一的篇幅所谓的“数学部分”完全是由格罗兹曼写的：


在格罗兹曼的神助攻下，爱因斯坦在同一篇paper的“物理部分”，写出了引力场方程的雏形：



按照今天的话说，上面的方程（11）左边是物质的能量动量张量，而右边是时空的度规形式。也就是说，物质的能量动量张量，是和时空的弯曲程度有关联的，它们之间的关联，我们可以用一个方程来表达， 这就是广义相对论里的爱因斯坦方程（按照爱因斯坦的思路，也就是广义相对论里的“泊松方程”）。
上面的公式（11）是爱因斯坦方程的最初形式，还不成熟，爱因斯坦还加上了“方程十有八九......”这样不确定的话。
又过了两年（1915年11月4日），爱因斯坦修改的引力场方程，还差了那么一点：


上面的方程左边是和时空的度规相关（学名是：里奇张量），右边是物质的能量动量张量。可惜还差了一点，这个方程是不完全的。
几天后11月11日，爱因斯坦在他的另外一篇短文里又修正了他的引力场方程为：


这里的 是推广了的里奇张量，被称为爱因斯坦张量。这个引力场方程已经和最终形式很像了，不过依旧是不完全的。
到了11月25日，爱因斯坦终于隆重推出了正确的引力场方程（如果读不懂不必太过纠结，当成外语看就好）：


撒花，祝贺，广义相对论引力场方程就此正式诞生。
那么问题来了。
为什么爱因斯坦从1913年格罗兹曼的神助攻之后，到1915年整整两年都没有推出引力场的方程，却在1915年11月突飞猛进，一下子大跃进地三次修正引力场方程，最后得到引力场方程的普遍形式的？
原因是：
1915年6月底到7月初，哥丁根的数学大师希尔伯特曾经让爱因斯坦去哥丁根给了长达十几个小时的关于广义相对论和引力论的报告。
希尔伯特是当时世界顶配的数学家，刚刚把兴趣转移到物理基础上。希尔伯特最好的基友，就是闵可夫斯基，可惜闵可夫斯基已经英年早逝了。现在希尔伯特接过闵可夫斯基空的班，想来捣鼓捣鼓物理。爱因斯坦滔滔不绝说了一堆物理，希尔伯特问道：小爱啊，你说了半天，引力场方程究竟在哪里呢？



希尔伯特

当爱因斯坦离开哥丁根后，希尔伯特和爱因斯坦继续保持交流，最后两人几乎同时推出了引力场方程。
就近是老希还是小爱先推出引力场方程，这就成为一段历史公案了。总之，爱因斯坦方程的更正确的叫法，应该叫爱因斯坦—希尔伯特方程。

引力场方程里的“宇宙常数”

爱因斯坦引力场方程是：


引力场方程最初的运用，是解释水星近动、光线偏折，预测引力波。接下来，人们用引力场方程推导出了球对称的引力场和黑洞的结构。
爱因斯坦同学意气风发，准备用引力场方程来求解整个宇宙的结构。但是他发现通过上面的方程，居然推出宇宙是动态的，不是在不停地膨胀，就是在不停地收缩，这和当时认为宇宙是稳态的、永恒的认识完全不符合滴。于是爱因斯坦在1917年被迫把自己的引力场方程修正成：


其中多出来的一个未知常数 ，被爱因斯坦称为“宇宙常数”。
到了1920年代，美国的天文学家哈勃发现，好家伙，所有的星系都在远离银河系。换句话说，我们的宇宙正在膨胀中。



哈勃，发现宇宙膨胀

爱因斯坦听说宇宙正在膨胀，于是去掉了他的宇宙常数，重新回到了之前的引力场方程，还宣传自己的宇宙常数真是一个“最大的错误”。
然而，几十年后，大自然再次告诉我们，这个宇宙真的有宇宙常数！爱因斯坦在引力场方程中去掉宇宙常数，这才是最大的错误。



1998年，两个美国天文学家（Adam Riess和Saul Perlmutter，图左边和中间的）领导的小组分别发现了我们的宇宙正在加速膨胀，这是一个惊人的发现，这两位老哥也和另一个澳大利亚的天文学家分享了2011年的诺贝尔物理学奖。
于是从1998年开始，宇宙学一度成为大火热的科学，如何把宇宙学里的参数测得精确一些成为了宇宙学主攻的实验观测方向，而成万上十万的各种维象理论被推出用来“解释”宇宙加速膨胀。
很可惜，热闹了一阵子，人们依旧不能理解宇宙的加速膨胀。不过爱因斯坦的宇宙学常数倒是被很好地测了出来：


别看这个数字貌似非常小，其实它对于宇宙来说相当大的，它对应了宇宙中俗语被称为“暗能量”（天文学家非常没有文化，没有好的词，用了什么暗能量暗物质的，非常粗鄙，一看就是好莱坞电影看多了。）
也就是说，宇宙常数就是暗能量，而宇宙中大概有68%的成分都是暗能量，暗能量的对外推斥造就了宇宙的加速膨胀。



虽然论文千千万， 但是没有人知道为什么宇宙中有68%的暗能量。估计很久以后也没人知道。宇宙常数究竟是什么，也无人知晓。
目前有一堆三脚猫的玄学理论，比如量子引力，比如随着时间变化的宇宙常数，可惜完全和观测实验不沾边，所以能算成哲学作品。
对爱因斯坦引力场方程的理解，依旧是很不充分的。

爱因斯坦对引力场方程满意吗？

答案是否定的。
按照爱因斯坦的原初想法，弯曲的时空可以通过坐标变换变回闵可夫斯基空间，也就是说，扭曲的时空和引力场是等价的。如果你依旧不理解，就可以想象一下，地球表面自由落体的参考系里没有引力，就是引力场变成没有引力场的一种坐标变换。
那么扭曲的时空是否也可以和电磁场等效起来？比如一个电荷辐射电磁场，是否可以通过坐标变换使得电荷的电磁场不见了，重新变回闵可夫斯基空间？
爱因斯坦在推出广义相对论后，就一直在思考这个问题。如果时空的扭曲等价于引力，那么怎么把时空的扭曲一分为二，一部分等价于引力，一部分等价于电磁场？貌似不可行。那么在黎曼时空外，多加一点料是否可以？
下面是爱因斯坦1929年的论文，试图把电磁场和引力场统一起来：


只可以没有了格罗兹曼和希尔伯特的神助攻，爱因斯坦没法搞出他的“远平行性”这个来自仿射几何学的概念。
再次尝试（1945年）：


当时还有好多数学家和物理学家跟着爱因斯坦的思路走，试图从几何学上入手，统一电磁场和引力场。可是，结果是失败的。
其中一个比较有趣的理论，是1921年由德国物理学家和数学家卡鲁扎整出来的“五维理论”。他认为只要在四维的黎曼流形之外再加上一个卷曲的第五维，如下：


就可以统一电磁场和引力场。爱因斯坦大喜，但是和卡鲁扎一算，乖乖，这个五维空间居然没有静态的球对称解，于是只能作罢。
由于经典的统一场论没有什么大进展，另一方面量子力学又突飞猛进，以至于人们开始嘲笑爱因斯坦“远离了学术主流”。爱因斯坦直到去世，经典的统一场论依旧没有进展，而电磁力、强力和弱力反而被统一了起来。再后来，人们又瞄准了卡鲁扎的五维理论，试图把维度加的更高，从而统一引力和其它三种力，这就是传说中的弦论。只可惜弦论到后来也没有什么进展，不过这是后话了。

相关阅读

我在别处的回答：
爱因斯坦为什么会有空间弯曲这种想法？
如何以哲学的角度理解时空的相对性？

原始资料
高斯《关于曲面的一般研究》https://www.gutenberg.org/files/36856/36856-pdf.pdf
黎曼《关于几何学的假设》https://www.emis.de/classics/Riemann/WKCGeom.pdf
爱因斯坦文集（主要看第二卷）https://book.douban.com/subject/6060527/

广相教科书们：写的简洁的，推荐狄拉克和俞允强的。写的优秀的，推荐温伯格的。写的初步的，推荐Schutz的。写的科普的，推荐我这篇。链接就不贴了。

一点补充

2021-6-16 根据评论加上了一点补充内容：
关于苹果落地：
很多朋友在评论里问到苹果落地的例子，这里再补充一些内容。
之所以举苹果的例子，是因为据说牛顿根据苹果落地，研究出了万有引力（这是伏尔泰编出来的故事）。这里的苹果，可以被抽象成一个"质点"，也就是只有质量而不计大小、形状的一个几何点。
我们回到最熟悉的牛顿第一运动定律：不受外力的物体，永远保持匀速直线运动或者是静止状态。
这条定律跑到广义相对论的框架下，就变成了：一个不受引力之外作用的物体（自由下落的物体）是按照四维时空的测地线运动的。如果用更物理化的方式描述，就是，一个“测试质点”在四维时空中，是沿着四维时空的测地线进行运动的。
在平直时空中，也就是没有引力的时空里，一个孤立的物体在平直时空里匀速直线运动，而这条“四维直线”被投影到三维空间里，就是一个点，或者也是一条匀速运动的直线，这个问题就转行回了牛顿第一运动定律。
现在我们考虑有地球引力的存在，在广义相对论的描述中，苹果（质点、物体，whatever）处在一个由于地球质量造成弯曲的四维时空中，在这个时空中沿着四维的测地线运动。请注意，在四维时空中，运动不是三维的“点”到“点”的运动，而是四维的“事件”到“事件”的运动，随着时间的流逝，物体必然会经历从时刻 t1 --> 时刻 t2，所以其必然扫过一条四维的曲线，而不可能在四维时空中静止不动。
所以，物体在四维时空中，永远走的是一条曲线（或者直线），这条曲线，我们可称之为物体的“世界线”。如果还是不理解，可以看一下下面的图，很有帮助，


注意这里空间被画成了两维，而时间在垂直的z轴。
而苹果走的“世界线”在三维空间的投影，恰好就是我们看到的苹果落地的运动。
有朋友问苹果在落下之前，为什么不走测地线运动，而固定在树上。这是一个好问题。
有两种解释。
第一种：我们说苹果走测地线运动，必须要求苹果是一个“自由运动”的苹果，也就是只受到引力作用的苹果。固定在树上的苹果，除了受到引力之外，还受到树枝的拉力，当然这是牛顿力学（静力学）的说法。从广义相对论来看，苹果在地球质量造成的弯曲时空里运动，显然还受到别的作用，并不是“自由运动”的，所以苹果走的不是测地线运动。
第二种解释更有趣。站在大树下，看苹果附近的空间。苹果除了受到地球引力之外，还受到树枝拉力，在广义相对论的框架下，树枝的拉力提供了另外一个作用，这个作用也会造成时空的弯曲。而树枝拉力造成的时空弯曲，恰好和地球质量造成的时空弯曲相抵消，所以，苹果是处在一个平直空间中，在三维空间中的表现就是——静止。
回到从空中落下的苹果。
这时候树枝的拉力不见了，树枝拉力对苹果周围造成的时空扭曲没有了，苹果沿着地球质量造成的弯曲时空走测地线。下面重点来了！如果把坐标系建立在苹果上，当然在苹果看来，自己依旧是三维空间静止的，自己处在一个平直时空中，走的是闵可夫斯基空间中的四维直线，没有受到任何引力场的作用。这就是广义相对论里的坐标变换，这样一变，地球的引力也被变“没”了。
引力可以通过坐标变换给产生出来，也可以通过坐标变换给消掉，这就体现了引力是时空的一种属性，也就是弯曲的时空产生引力的效果。

关于光线偏折：
这里再补充一下，关于牛顿力学下计算光线弯曲的问题，为什么算出来是广义相对论算出来的一半。
首先，在牛顿力学下，光线在引力场中弯曲具有一个前提假设，即光是一种具有质量的颗粒（牛顿光的微粒说），所以光在太阳附近的运动是一条（三维空间里）双曲线运动。
后来，光的微粒说被光的波动说取代，按照波动说，光在太阳附近是不会弯曲的。
在广义相对论的框架下，光依旧是没有质量的，所以光走的完全不是三维空间里的双曲线运动，连近似也不是。光走的是太阳附近引力场的测地线运动，而这个运动的空间分量，和双曲线运动相差很大。
所以，广义相对论框架下计算出来的光在引力场中的弯曲，和牛顿力学计算出来的相差很大。至于为什么差了两倍，一个定性的解释是，牛顿力学只考虑了时间的弯曲，而空间依旧是平直的。广义相对论同时考虑了时间和空间的弯曲，而对于光来说，空间和时间造成了相同量的弯曲，所以恰好是牛顿力学结果的两倍。
其次讨论了一下为什么牛顿力学算出来太阳附近的光线偏转是广义相对论的一半。其实如果按照光的波动说，光线是完全不偏转的。牛顿力学把光当成具有质量的颗粒，在太阳附近做双曲线运动。也补充在了原文里。

另外一些补充：
第三，有人提到不是质量使得时空弯曲，而是物质的能量动量张量使得时空弯曲。很对。不过我在文章已经提到了。（这里有一个相对论的open question，不过在这里先不提了。）
第四，有哥们说我偷偷在文里鄙视天文学家粗鄙，谢谢那位兄弟看得这么仔细。为了防止人看不到，那我就放到最后划重点鄙视一下：
天文学家非常没有文化，没有好的词，用了什么暗能量暗物质的，非常粗鄙，一看就是好莱坞电影看多了。
其实从“大爆炸”这个词开始，就已经很没文化了。“大爆炸”本来是Fred Hoyle反对这个理论而给它取的绰号。本来加莫夫把这个理论叫做 理论，还有点意思。当初John Wheeler（费曼的老板）搞出“黑洞”这个词，直接被人骂没文化。结果Wheeler直接说“黑洞无毛”，被人直骂下流。

简单回答楼主的疑问。
就按楼主说的【空间弯曲】（其实广义相对论指的是时空弯曲）
首先请楼主将自己视为上帝，造了一种球面，在球面上造了一种“片状生物”，这些生物的视觉只能贴着球面走（比如其视觉来源是面上的某种信号介质），他们早期的认知也是局限在球面
由于球面很大，他们在初期，科技不发达，他们发明的【二维测量仪器】精度也不高，因此发展出几何学时，他们用自己的天生器官，还是精度不高的仪器，得到的结果有【平行线不相交】【三角形内角和为180°】【圆周率为π】等，因此他们认为，他们的宇宙空间是【平直】的。
注意，他们只知道是【平直】，但不知道是【平面】，因为他们没有第三维认知，我们一旦说【面】，这是作为我们上帝视角看到的
为什么他们会以为他们的宇宙【平直】，因为从我们上帝视角，很简单，因为
球面太大，小范围都近似平面，由于他们初期活动范围小，虽然他们没有第三维认知，但通过他们的观察测量，发现他们自己的这个二维宇宙空间的全部测量性质都是满足【数学上或几何上二维平直空间】性质的，所以他们理所当然认为【宇宙是平直的】
也就是说，虽然他们没有第三维认知，是二维生物，但他们完全可以通过【测量】【推导】他们的宇宙是什么形态，平直，还是弯曲
在今后的几百年，他们这种基于【宇宙平直】的物理学，都用的很好。
但他们之中也有逻辑思维发达的物理学家，总觉得理论不够完备，为什么呢？因为【平直】是仪器测出的，仪器是有精度的，所以【平直】归根到底是测出来，或者观测出来的，不是推导出来的
随着他们的科技发展，一方面他们活动范围进一步增大，可以跨越半个球面。这时再用仪器测，发现问题了
什么问题呢，比如他们在他们的宇宙中，取三个点，然后连成【直线】。这个【直线】，在我们上帝视角，其实就是大圆弧，而他的视角，还是按他们几个学对直线的定义：两点之间最短的线。
注意，他们是不可能知道这是【大圆弧】的，那是我们有第三维认知说的，这对他们的认知，就是【直线】
然后他们用【他们自己的二维量角器】，测三个角，加起来，居然不是180°！
神奇了，进一步比如，大范围，两条平行线，也相交了。比如赤道取两点（赤道是我们说的，他们只是说直线上取两点），作垂线，画到北极（我们说的），居然交在了一起。
还有许多不可思议的现象。。。
我们对上述现象很容易理解，因为这是【球面】，球面上他们说的【直线】，我们知道不过是【大圆弧】
但他们无法理解什么是【大圆弧】，他们只能通过观测，发现发生了上述怪事
于是他们的科学家开始问为什么？结果有科学家提出，【也许我们的宇宙并不平直，过去以为平直，仅仅是我们的天然器官或仪器精度不够的误解，我们本来就生活在一个弯曲宇宙空间】，因此【过去基于平直假设的物理学，要全部推翻，重新建立】
看到没？虽然他们没有第三维认知，但通过测量，也有可能建立一套【弯曲宇宙的几何学，并基于该几何学建立一套完全不同的物理学】
现在请楼主把身份转换回来，把我们想成类似这些生物，不过呢，我们的空间认知是三个维度
我们为什么过去觉得我们宇宙平直呢？和他们一样，我们只不过高一维，在空间取三个点，连直线，内角和也是180°，空间中画个圆圆周率也是π。。。。空间中的一切性质【似乎】都符合平直几何学，也就是我们中学学的欧几里得几何
但有了前面的故事，你能保证在大尺度，比如几亿光年跨度的三角形内角和也是180°？或者说，就算在你身边画个小三角形，量角器如何精度精确到小数点20位，内角和还是180°？或者，毕竟在地球附近你觉得这样，那大质量天体，中子星或黑洞附近也是吗？
因此，不能通过【观测】就说肯定如此，如果有一种理论，能直接【推导】出来更好
这个理论，名字叫【广义相对论】。
【广义相对论】比上述故事更好的一点，在于上述故事是他们这些“片状”生物科技足够发达，活动范围大到跨越半个球面，直接通过观测发现宇宙不平直的
而广义相对论，是在我们还不能活动到几百万光年去画三角形，我们的仪器精度，科技还不够条件下，直接推导出了我们的宇宙空间是【弯曲的】
这对广义相对论，是一种预言
这种预言，目前检验它很困难。为什么？因为我们生活的太阳系，是【近似】平直空间。我们仪器精度没那么高，测不出这点弯曲。
不过好就好在，有些极端天文观测证实了这点，如引力红移，水星偏折，还有上两个月人类拍摄的黑洞。相信这些验证现象随科技发现越来越多。
至于【我们宇宙空间是弯曲的】如何推导呢？我这里不说了
因为楼主只是问，【空间弯曲是什么意思】，而不是【空间为什么弯曲】，如果要想知道，请系统学习广义相对论
而楼主问的，为什么引力效应是空间弯曲（其实是时空弯曲）表现，因为广义相对论推导出，【自由粒子沿短程线运动】
这个短程线，在弯曲时空就是两点距离最短的线。不过注意，这是包括时间坐标在内的【四维世界线】，不是【三维空间轨迹】
无论苹果加速下落，还是星球公转，都是【四维短程线】在你的眼睛看到的【三维空间投影轨迹】
进一步给楼主说下，地面附近，由时空形态导出的短程线轨迹，投影到三维空间，其加速度就是近似9.8m/s^2
不过具体，楼主请系统学习，广义相对论
回答完毕